The Perils of Exponential Growth
- vicluca
- Sep 12, 2019
- 6 min read
Updated: Apr 29, 2022
Victor Luca, 12-Sep-19.
Published in The Beacon, 28-Jan-20
The math is simple but folk just don't seem to appreciate or understand exponential growth.
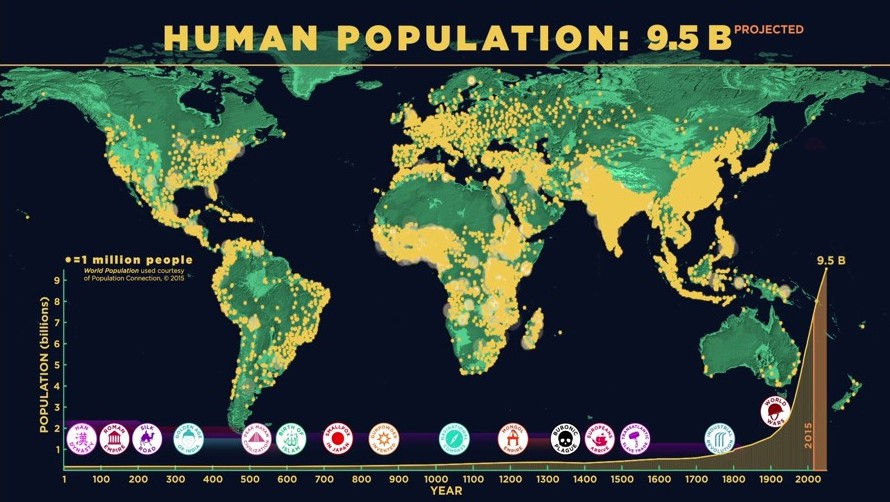
Source: Human Population Through Time, American Museum of Natural History.
It may seem strange to some readers that I start this article on the future of humanity with an explanation of compound interest. Please bear with me as I attempt to demonstrate the implications of a quantity that is steadily accumulating at a constant rate.
If I deposit say $100 in a bank account that returns an interest rate of 10% per annum, then after the 1st year I would have $110. After the 2nd year I would have $121, after the 3rd year $133 and so on until after the 7th year I have approximately doubled my money. I double my money again by year 14 and every seven years after that. So the doubling time for a quantity (in our case $) that is increasing at 10% per annum is 7 years. Below is a graph of the amount of money I have versus years from my first deposit. It can be seen that for the first 60 years or so little or nothing seems to be happening. Then all of a sudden the curve takes off and heads skyward.
Warren Buffet (the CEO of Berkshire Hathaway) is the world’s third richest man and he has made most of his fortune by investing in good low-risk companies that grow by making a cash return of roughly 10% per annum. From early on he understood the power of the simple math I have described. It is astonishing how quickly someone like Buffet has been able to become enormously rich with a modest initial investment and modest growth rates.
In mathematical parlance the graph shown above is known as an exponential function. It looks a bit like a hockey stick if I go out a long way in time. The amount that is accumulating (the $) is shooting off into infinity as we go out in time.
The exponential function can be described by the following general equation:
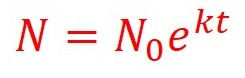
In this equation N is a quantity that is accumulating (the $) and N0 is the amount of the initial deposit in dollars, or $100 in our compound interest example. The symbol k represents a constant value known as the growth rate (in %). In our case this is the interest rate of 10% per annum and it doesn’t change year-on-year. t is the time in years and t = 0 is start time. The constant, k, has the value:

Here T2 is the time required for the quantity to double, the doubling time that I referred to above. Since the natural logarithm of 2 (ln(2)) is approximately 70, then if we know the growth rate of the quantity in %, we can calculate the time for the bank balance or some other quantity to double. We did the basic math above.
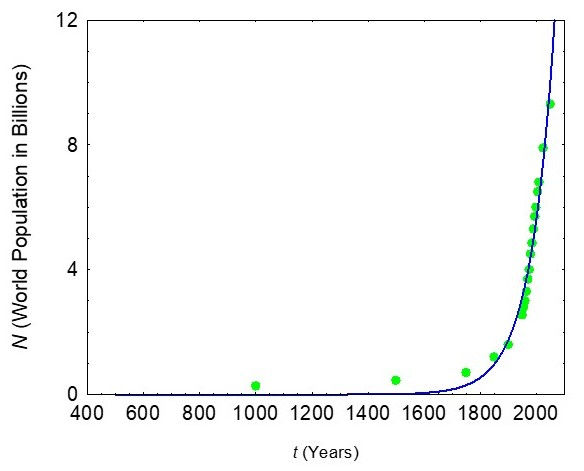
The exponential function also approximates the increase in human population with time as shown in the graph below. This is the famous hockey stick curve and is one of the major underlying problems of climate change. Since human population is increasing exponentially, so too does food consumption and the generation of waste etc.
The increase in carbon dioxide (CO2) and other green-house gas emissions in the atmosphere and global average temperatures are also following a hockey stick curve or exponential function.
Following on from what we said before, but changing the numbers a bit, if the growth rate is 3%, then any quantity undergoing exponential growth would double in 23 years. A growth rate of 5% would result in doubling every 14 years. I guess you get the idea?
What I am trying to show here is that modest rates of growth can give astonishingly short doubling times.
Now let’s look at something a bit closer to home. For much of Aotearoa’s recent history we have had an average annual population growth rate of about 1.3%. As I have already explained a 1.3% growth rate in population would give a doubling time of about 70/1.3, or about 54 years. As you can see from the graph shown below that was compiled from data from StatsNZ, this is about right. From 1926 to about 1976, the population went from 1.42 million to about 3.1 million which is about as expected. In recent times, mostly due to the government’s aggressive migration program, annual population increase has been about 2%. This corresponds to a population doubling time of 70/2 or 35 years. If we continued the graph out further in time it would eventually also look like a hockey stick.
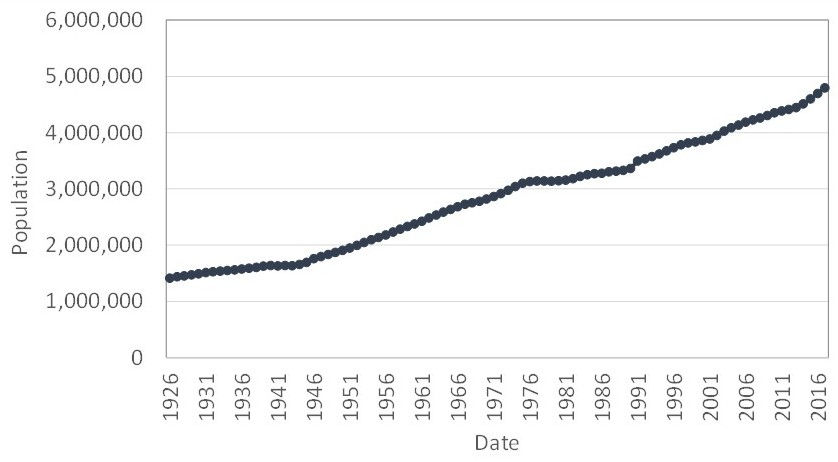
Aotearoa’s population growth from 1926 to 2016.
Exponential decline is very similar to exponential growth only instead of the hockey sick increasing with time it goes the other way, it decreases with time, rapidly at first and then more slowly. Exponential decline could be applied for instance to a fixed resource that is being depleted at a constant rate. Exponential decay also happens to describe the phenomenon of radioactive decay.
Again, the important point here is that very modest growth or consumption rates can lead to the frighteningly fast explosion in say a population or the exhaustion of a resource.
Let’s now take another example of exponential growth that dates back to ancient times.

The game of chess probably originated in India and Persia. Legend has it that the court mathematician of the King of ancient Persia was very pleased with the inventor of chess, a mathematician, and offered to reward the mathematician anything he wanted because the King wasn’t a very smart individual and assumed that all the sly mathematician wanted was money.
A simplified form of the equation above that describes the situation is given by this simple exponential equation where N is the number of grains of wheat:

According to this legend, the reward that the mathematician wanted was for the King to put one grain of wheat on the first square of his chess board, two grains on the second, four on the third, eight on the fourth, and so on. That is, a doubling of wheat on each square. “Very well,” the King probably said. He most likely didn’t see the consequences of his actions because he was too preoccupied with taxing the peasants and pillaging nearby villages.
Since there are 64 squares on the chess board the total amount of grain evaluates to N = 264. That is, N = 2x2x2x2… repeated 64 times. This is an unimaginably humungous number. As it happened there was not that much grain in the entire world.
A nice little riddle that also demonstrates the exponential function is that of the lily pond. The pond initially contains one lily pad and that doubles every day. If it takes thirty days to completely fill the pond then how long does it take to half fill the pond? The answer is 29 days. It took 29 days to half fill the pond, but on the thirtieth day it went from half full to completely full. Dramatic isn’t it?
Professor Albert Bartlett (1923-2013) was Emeritus Professor at the Department of Physics, University of Colorado at Boulder and for many years he taught his undergraduate students about the exponential function (https://en.wikipedia.org/wiki/Albert_Allen_Bartlett). He regularly made the following statement.
"The greatest shortcoming of the human race is our inability to understand the exponential function."
Some of his classes can be viewed on You Tube. Part 1 can be found at the following address:
This video has been viewed over five million times. Way less than Taylor Swift’s song “Shake it Off” that has been viewed 2.8 billion times. I would argue that Bartlett’s math is far, far more important for the future of humanity than Swift’s video, entertaining as it might be. I have watched her video several times myself, just as I have watched Bartlett’s.
After years of thinking about the exponential function Prof. Bartlett came to the conclusions listed below. These conclusions are to be found in his article in the American Journal of Physics, September 1978.
It doesn’t matter if the reader does not understand the math I presented above as long as the reader appreciates that the conclusions that are to be reached from an understanding of such a simple mathematical expression are inescapable. In his article
Bartlett makes the following conclusions on what we MUST do:
(i) Educate all of our people to an understanding of the arithmetic and consequences
of growth. "The promotion of growth is simply a sophisticated way to steal from our children." - David Brower (a famous environmentalist).
(ii) Conserve in the use and consumption of everything. We must outlaw planned
obsolescence. We must recognize that, as important as it is to conserve, the arithmetic shows clearly that large savings from conservation will be wiped out in short times by even modest rates of growth.
(iii) Recycle almost everything.
(iv) Invest great sums in research (a) to develop the use of solar, geothermal, wind,
tidal, biomass, and alternative energy sources; (b) to reduce the problems of nuclear fission power plants; (c) to explore the possibility that we may be able to harness nuclear fusion.
(v) Recognize that it is exceedingly unscientific to promote ever-increasing rates of
consumption of our fuel resources based on complete confidence that science, technology,
and the economics of the marketplace will combine to produce vast new energy resources
as they are needed.
(vi) Not sit back and deplore the lack of "leadership”. We must show leadership ourselves.
More than forty years have passed since Bartlett penned his article and the advice he gave is more important today than ever before.
I invite readers to think hard about what has been written here because it is critical in understanding the plight that humanity faces. The math leads you to only one conclusion and that is that growth is no panacea, but rather the cause of many of our problems. Now go and tell that to your CEO and the market-based economic system that dominates our lives. Do the Math!



Comments